Prepare Greenberger–Horne–Zeilinger state with Quantum Circuit

First, you have to use this package in Julia.

using Yao, Yao.Blocks

Then let's define the oracle, it is a function of the number of qubits. The circuit looks like this:

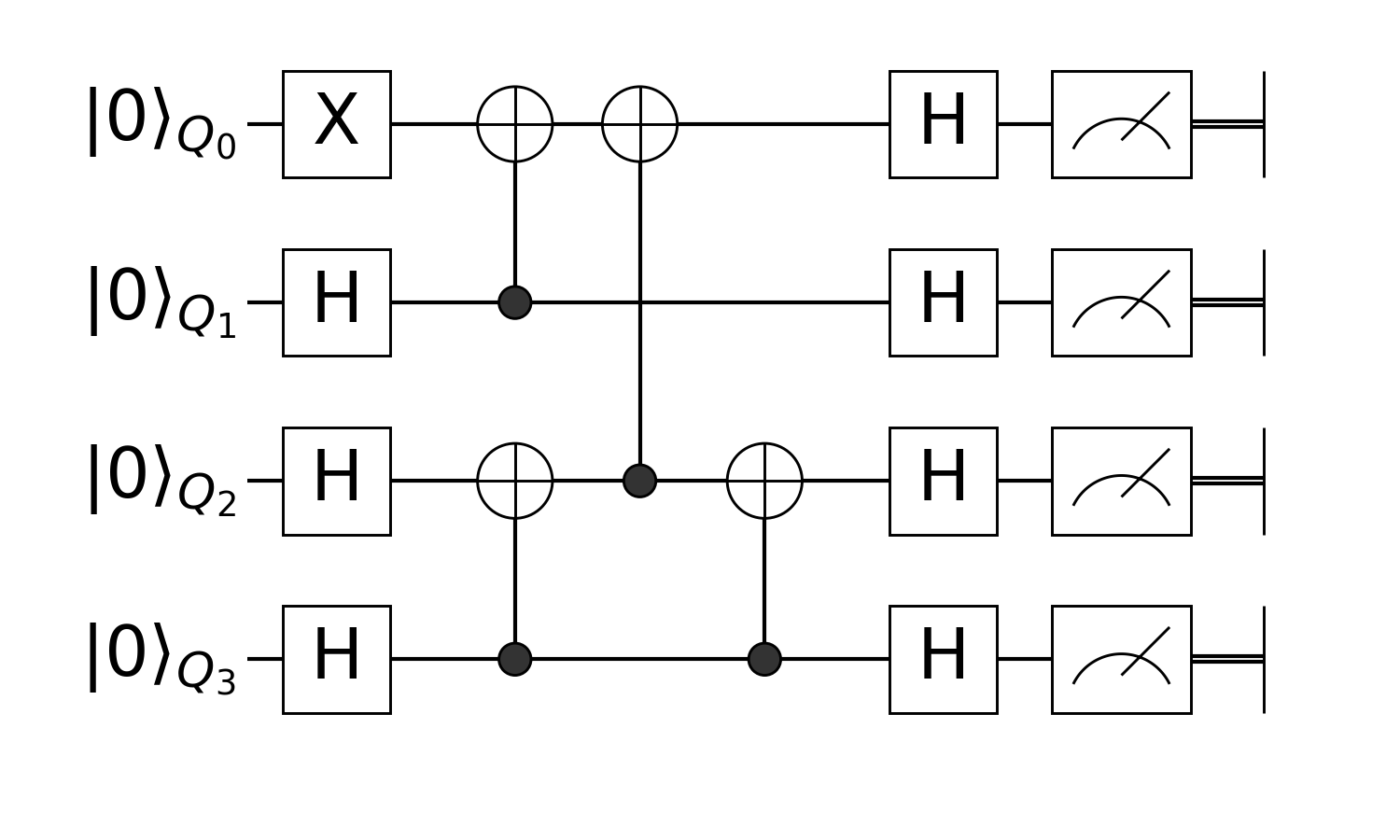
n = 4
circuit(n) = chain(
    n,
    put(1=>X),
    repeat(H, 2:n),
    control(2, 1=>X),
    control(4, 3=>X),
    control(3, 1=>X),
    control(4, 3=>X),
    repeat(H, 1:n),
)

circuit (generic function with 1 method)

Let me explain what happens here. Firstly, we have an X gate which is applied to the first qubit. We need decide how we calculate this numerically, Yao offers serveral different approach to this. The simplest one is to use put(n, ibit=>gate) to apply a gate on the register. The first argument n means the number of qubits, it can be lazy evaluated.

put(n, 1=>X) == put(1=>X)(n)

true

If you wanted to apply a two qubit gate,

put(n, (2,1)=>CNOT)

Total: 4, DataType: Complex{Float64}
put on (2, 1)
└─ CNOT gate

However, this kind of general apply is not as efficient as the following statement

mat(put(n, (2,1)=>CNOT)) ≈ mat(control(n, 2, 1=>X))

true

This means there is a X gate on the first qubit that is controled by the second qubit. Yao.jl providea a simple API mat to obtain the matrix representation of a block SUPER efficiently. This distinct feature helps users debug their quantum programs easily, and is equally useful in time evolution and ground state solving problems.

For a multi-controlled gate like Toffoli gate, the construction is quite intuitive

control(n, (2, 1), 3=>X)

Total: 4, DataType: Complex{Float64}
control(2, 1)
└─ (3,)=>X gate

Do you know how to construct a general multi-control, multi-qubit gate? Just have a guess and try it out!

In the begin and end, we need to apply H gate to all lines, you can do it by repeat, For some specific types of gates such as X, Y and Z, applying multiple of them can be as efficient as applying single gate.

The whole circuit is a chained structure of the above blocks. And we actually store a quantum circuit in a tree structure.

circuit

circuit (generic function with 1 method)

After we have an circuit, we can construct a quantum register, and input it into the oracle. You will then receive this register after processing it.

r = apply!(register(bit"0000"), circuit(4))

DefaultRegister{1, Array{Complex{Float64},2}}
    active qubits: 4/4

Let's check the output:

statevec(r)

16-element Array{Complex{Float64},1}:
  0.7071067811865471 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
                 0.0 + 0.0im
 -0.7071067811865471 + 0.0im

We have a GHZ state here, try to measure the first qubit

measure(r, nshot=1000)

1000-element Array{Int64,1}:
  0
 15
  0
 15
 15
 15
  0
 15
 15
  0
  ⋮
  0
 15
 15
 15
 15
 15
 15
 15
 15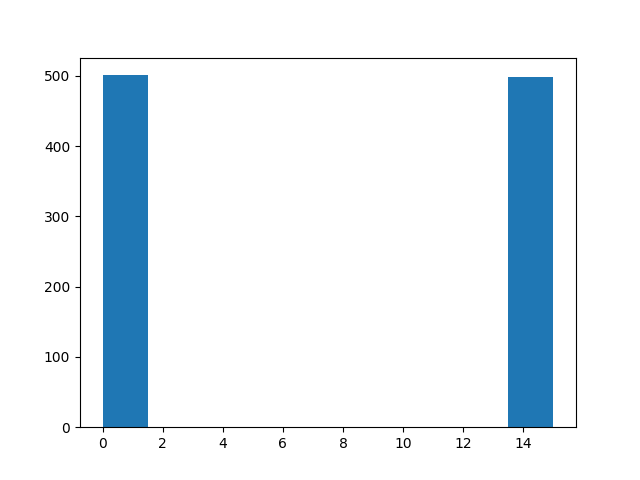

GHZ state will collapse to $|0000\rangle$ or $|1111\rangle$ due to entanglement!

This page was generated using Literate.jl.