Quantum Fourier Transformation and Phase Estimation
Quantum Fourier Transformation
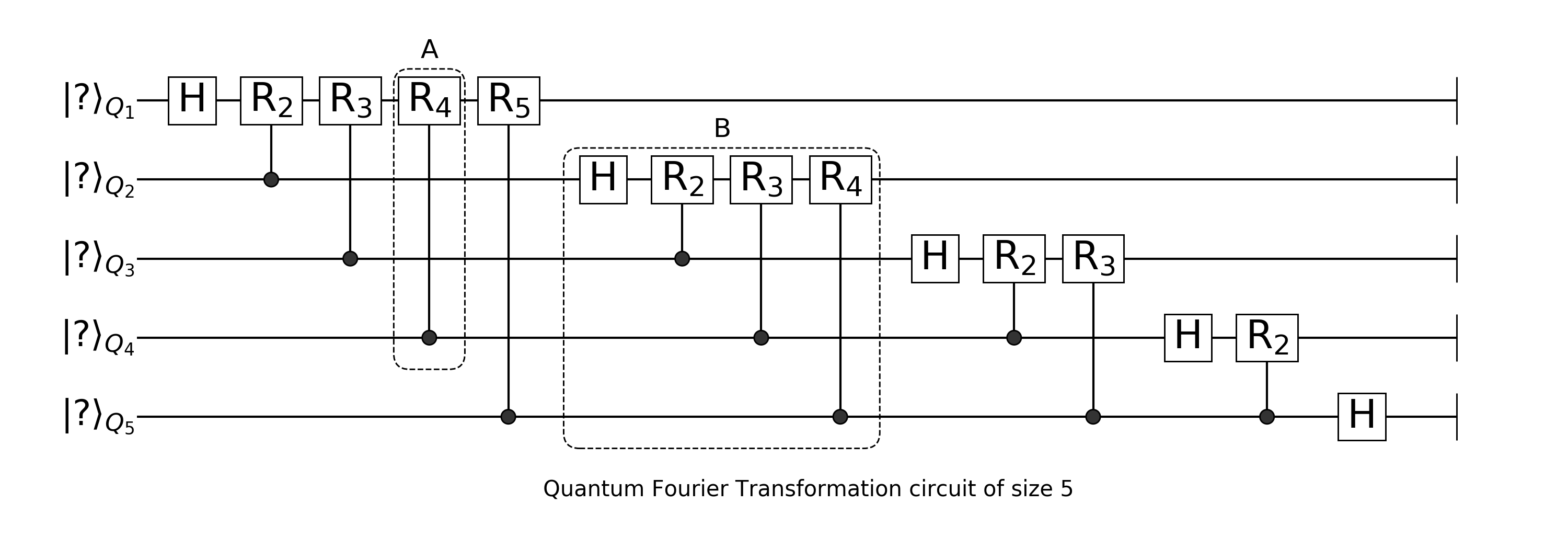
using Yao
# Control-R(k) gate in block-A
A(i::Int, j::Int, k::Int) = control([i, ], j=>shift(2π/(1<<k)))
# block-B
B(n::Int, i::Int) = chain(i==j ? kron(i=>H) : A(j, i, j-i+1) for j = i:n)
QFT(n::Int) = chain(n, B(n, i) for i = 1:n)
# define QFT and IQFT block.
num_bit = 5
qft = QFT(num_bit)
iqft = qft' # get the hermitian conjugateTotal: 5, DataType: Complex{Float64}
chain
├─ chain
│ └─ kron
│ └─ 5=>H gate
├─ chain
│ ├─ control(5)
│ │ └─ (4,)=>Phase Shift Gate:-1.5707963267948966
│ └─ kron
│ └─ 4=>H gate
├─ chain
│ ├─ control(5)
│ │ └─ (3,)=>Phase Shift Gate:-0.7853981633974483
│ ├─ control(4)
│ │ └─ (3,)=>Phase Shift Gate:-1.5707963267948966
│ └─ kron
│ └─ 3=>H gate
├─ chain
│ ├─ control(5)
│ │ └─ (2,)=>Phase Shift Gate:-0.39269908169872414
│ ├─ control(4)
│ │ └─ (2,)=>Phase Shift Gate:-0.7853981633974483
│ ├─ control(3)
│ │ └─ (2,)=>Phase Shift Gate:-1.5707963267948966
│ └─ kron
│ └─ 2=>H gate
└─ chain
├─ control(5)
│ └─ (1,)=>Phase Shift Gate:-0.19634954084936207
├─ control(4)
│ └─ (1,)=>Phase Shift Gate:-0.39269908169872414
├─ control(3)
│ └─ (1,)=>Phase Shift Gate:-0.7853981633974483
├─ control(2)
│ └─ (1,)=>Phase Shift Gate:-1.5707963267948966
└─ kron
└─ 1=>H gateThe basic building block - controled phase shift gate is defined as
In Yao, factory methods for blocks will be loaded lazily. For example, if you missed the total number of qubits of chain, then it will return a function that requires an input of an integer. So the following two statements are equivalent
control([4, ], 1=>shift(-2π/(1<<4)))(5) == control(5, [4, ], 1=>shift(-2π/(1<<4)))trueBoth of then will return a ControlBlock instance. If you missed the total number of qubits. It is OK. Just go on, it will be filled when its possible.
Once you have construct a block, you can inspect its matrix using mat function. Let's construct the circuit in dashed box A, and see the matrix of $R_4$ gate
julia> a = A(4, 1, 4)(5)
Total: 5, DataType: Complex{Float64}
control(4)
└─ 1=>Phase Shift Gate:-0.39269908169872414
julia> mat(a.block)
2×2 Diagonal{Complex{Float64}}:
1.0+0.0im ⋅
⋅ 0.92388-0.382683imSimilarly, you can use put and chain to construct PutBlock (basic placement of a single gate) and ChainBlock (sequential application of MatrixBlocks) instances. Yao.jl view every component in a circuit as an AbstractBlock, these blocks can be integrated to perform higher level functionality.
You can check the result using classical fft
# if you're using lastest julia, you need to add the fft package.
using FFTW: fft, ifft
using LinearAlgebra: I
using Test
@test chain(num_bit, qft, iqft) |> mat ≈ I
# define a register and get its vector representation
reg = rand_state(num_bit)
rv = reg |> statevec |> copy
# test fft
reg_qft = apply!(copy(reg) |>invorder!, qft)
kv = ifft(rv)*sqrt(length(rv))
@test reg_qft |> statevec ≈ kv
# test ifft
reg_iqft = apply!(copy(reg), iqft)
kv = fft(rv)/sqrt(length(rv))
@test reg_iqft |> statevec ≈ kv |> invorderQFT and IQFT are different from FFT and IFFT in three ways,
- they are different by a factor of $\sqrt{2^n}$ with $n$ the number of qubits.
- the little end and big end will exchange after applying QFT or IQFT.
- due to the convention, QFT is more related to IFFT rather than FFT.
Phase Estimation
Since we have QFT and IQFT blocks we can then use them to realize phase estimation circuit, what we want to realize is the following circuit 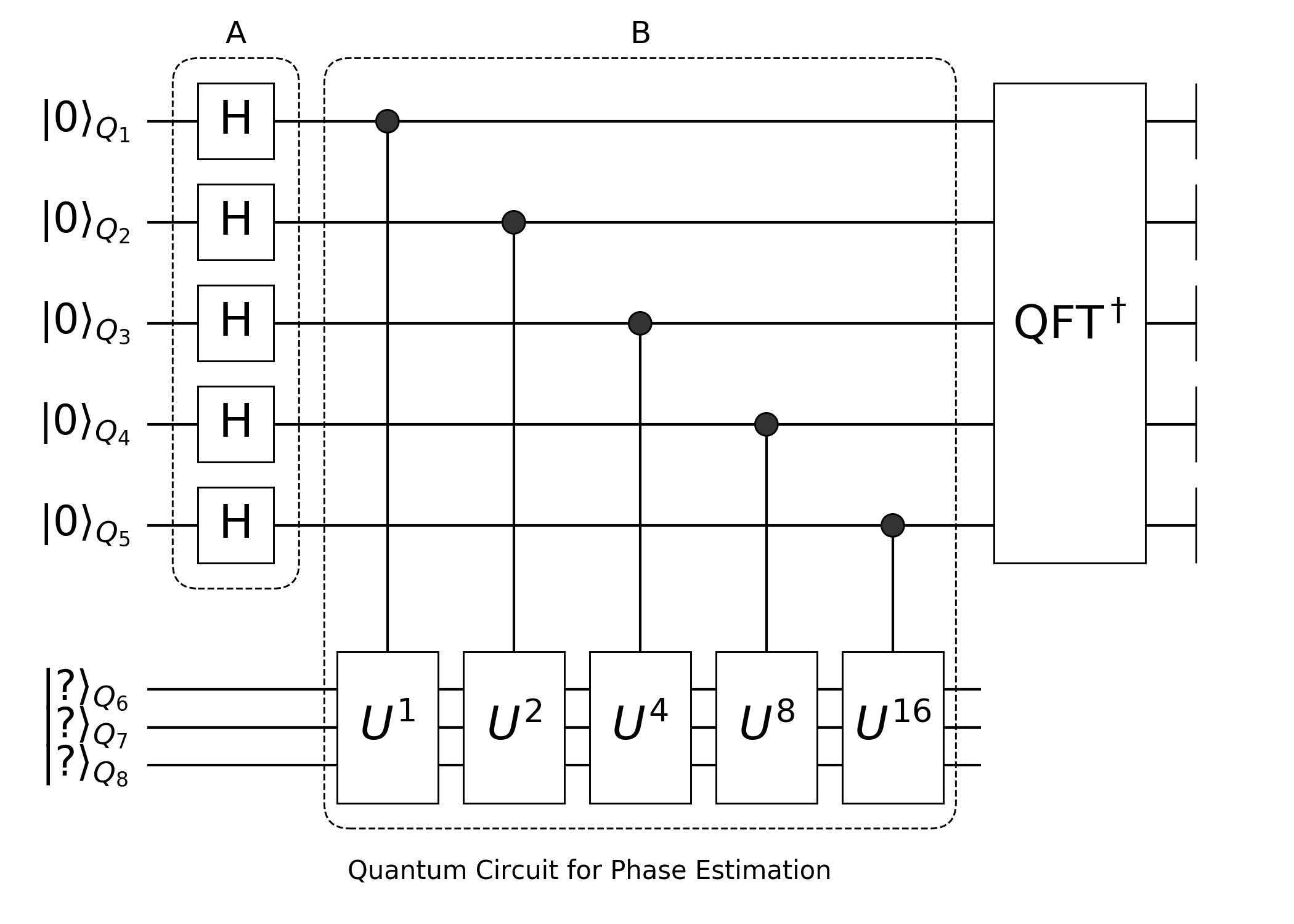
In the following simulation, we use equivalent QFTBlock in the Yao.Zoo module rather than the above chain block, it is faster than the above construction because it hides all the simulation details (yes, we are cheating :D) and get the equivalent output.
using Yao
using Yao.Blocks
using Yao.Intrinsics
function phase_estimation(reg1::DefaultRegister, reg2::DefaultRegister, U::GeneralMatrixGate{N}, nshot::Int=1) where {N}
M = nqubits(reg1)
iqft = QFT(M) |> adjoint
HGates = rollrepeat(M, H)
control_circuit = chain(M+N)
for i = 1:M
push!(control_circuit, control(M+N, (i,), (M+1:M+N...,)=>U))
if i != M
U = matrixgate(mat(U) * mat(U))
end
end
# calculation
# step1 apply hadamard gates.
apply!(reg1, HGates)
# join two registers
reg = join(reg1, reg2)
# using iqft to read out the phase
apply!(reg, sequence(control_circuit, focus(1:M...), iqft))
# measure the register (on focused bits), if the phase can be exactly represented by M qubits, only a single shot is needed.
res = measure(reg; nshot=nshot)
# inverse the bits in result due to the exchange of big and little ends, so that we can get the correct phase.
breflect.(M, res)./(1<<M), reg
endphase_estimation (generic function with 2 methods)Here, reg1 ($Q_{1-5}$) is used as the output space to store phase ϕ, and reg2 ($Q_{6-8}$) is the input state which corresponds to an eigenvector of oracle matrix U. The algorithm detials can be found here.
In this function, HGates corresponds to circuit block in dashed box A, control_circuit corresponds to block in dashed box B. matrixgate is a factory function for GeneralMatrixGate.
Here, the only difficult concept is focus, focus returns a FunctionBlock, that will make focused bits the active bits. An operator sees only active bits, and operating active space is more efficient, most importantly, it becomes much easier to integrate blocks. However, it has the potential ability to change line orders, for safety consideration, you may also need safer Concentrator.
r = rand_state(6)
apply!(r, focus(4,1,2)) # or equivalently using focus!(r, [4,1,2])
nactive(r)3Then we will have a check to above function
using LinearAlgebra: qr, Diagonal
rand_unitary(N::Int) = qr(randn(N, N)).Q
M = 5
N = 3
# prepair oracle matrix U
V = rand_unitary(1<<N)
phases = rand(1<<N)
ϕ = Int(0b11101)/(1<<M)
phases[3] = ϕ # set the phase of the 3rd eigenstate manually.
signs = exp.(2pi*im.*phases)
U = V*Diagonal(signs)*V' # notice U is unitary
# the state with phase ϕ
psi = U[:,3]
res, reg = phase_estimation(zero_state(M), register(psi), GeneralMatrixGate(U))
println("Phase is 2π * $(res[]), the exact value is 2π * $ϕ")Phase is 2π * 0.5, the exact value is 2π * 0.90625